A charged particle going around in a circle can be considered to be a current loop. A particle of mass m carrying charge $q$ is moving in a plane with speed $\mathrm{v}$ under the influence of magnetic field $\overrightarrow{\mathrm{B}}$. The magnetic moment of this moving particle:
Correct Option: , 4
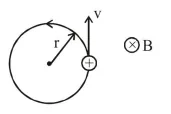
Magnetic moment
$\mathrm{M}=\mathrm{iA}$
$M=\left(\frac{q}{T}\right) \times \pi r^{2}=\frac{q \pi r^{2}}{\left(\frac{2 \pi r}{v}\right)}=\frac{q v r}{2}$
$\mathrm{M}=\frac{\mathrm{qv}}{2} \times \frac{\mathrm{vm}}{\mathrm{qB}}$
$\mathrm{M}=\frac{\mathrm{mv}^{2}}{2 \mathrm{~B}}$
As we can see from the figure, direction of magnetic moment (M) is opposite to magnetic field.
$\overrightarrow{\mathrm{M}}=-\frac{\mathrm{mv}^{2}}{2 \mathrm{~B}} \hat{\mathrm{B}}$
$=-\frac{\mathrm{mv}^{2}}{2 \mathrm{~B}^{2}} \overrightarrow{\mathrm{B}}$
