A charged particle of mass ' $m$ ' and charge ' $q$ ' moving under the influence of uniform electric field $E \hat{i}$ and a uniform magnetic field $B \vec{k}$ follows a trajectory from point $\mathrm{P}$ to $\mathrm{Q}$ as shown in figure. The velocities at $\mathrm{P}$ and $\mathrm{Q}$ are respectively, $v \vec{i}$ and $-2 v \vec{j}$. Then which of the following statements $(A, B, C, D)$ are the correct? (Trajectory shown is schematic and not to scale)
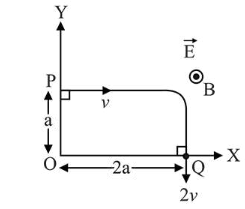
(A) $\mathrm{E}=\frac{3}{4}\left(\frac{m v^{2}}{q a}\right)$
(B) Rate of work done by the electric field at $\mathrm{P}$ is $\frac{3}{4}\left(\frac{m v^{2}}{a}\right)$
(C) Rate of work done by both the fields at $\mathrm{Q}$ is zero
(D) The difference between the magnitude of angular momentum of the particle at $\mathrm{P}$ and $\mathrm{Q}$ is 2 mav.
Correct Option: , 3
(3) (A) By work energy theorem
$W_{m g}+W_{\text {ele }}=\frac{1}{2} m(2 v)^{2}-\frac{1}{2} m(v)^{2}$
$0+q E_{0} 2 a=\frac{3}{2} m v^{2}$
$\Rightarrow E_{0}=\frac{3}{4} \frac{m v^{2}}{q a}$
(B) Rate of work done at $P=$ power of electric force
$=q E_{0} V=\frac{3}{4} \frac{m v^{3}}{a}$
(C) At, Q, $\frac{d w}{d t}=0$ for both the fields
(D) The difference of magnitude of angular momentum of the particle at $P$ and $Q$,
$\Delta \vec{L}=(-m 2 v 2 a \hat{k})-(-m v a \hat{k})$
$|\Delta \vec{L}|=3 \mathrm{mva}$
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.
