Question.
A chord of a circle is equal to the radius of the circle. Find the angle subtended by the chord at a point on the minor arc and also at a point on the major arc.
Solution:
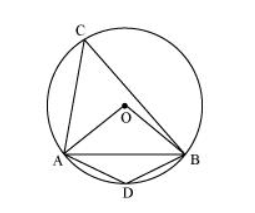
In $\triangle O A B$
$A B=O A=O B=$ radius
$\therefore \triangle O A B$ is an equilateral triangle.
Therefore, each interior angle of this triangle will be of $60^{\circ}$.
$\therefore \angle A O B=60^{\circ}$
$\angle \mathrm{ACB}=\frac{1}{2} \angle \mathrm{AOB}=\frac{1}{2}\left(60^{\circ}\right)=30^{\circ}$
In cyclic quadrilateral ACBD,
$\angle A C B+\angle A D B=180^{\circ}$ (Opposite angle in cyclic quadrilateral)
$\Rightarrow \angle A D B=180^{\circ}-30^{\circ}=150^{\circ}$
Therefore, angle subtended by this chord at a point on the major arc and the minor arc are 30° and 150° respectively.
In $\triangle O A B$
$A B=O A=O B=$ radius
$\therefore \triangle O A B$ is an equilateral triangle.
Therefore, each interior angle of this triangle will be of $60^{\circ}$.
$\therefore \angle A O B=60^{\circ}$
$\angle \mathrm{ACB}=\frac{1}{2} \angle \mathrm{AOB}=\frac{1}{2}\left(60^{\circ}\right)=30^{\circ}$
In cyclic quadrilateral ACBD,
$\angle A C B+\angle A D B=180^{\circ}$ (Opposite angle in cyclic quadrilateral)
$\Rightarrow \angle A D B=180^{\circ}-30^{\circ}=150^{\circ}$
Therefore, angle subtended by this chord at a point on the major arc and the minor arc are 30° and 150° respectively.