A chord PQ of a circle of radius 10 cm subtends an angle of 60° at the centre of the circle.

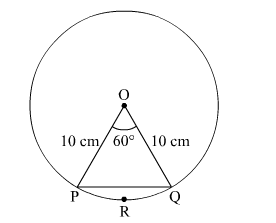
Radius of the circle, r = 10 cm

Area of sector $O P R Q$

$=\frac{60^{\circ}}{360^{\circ}} \times \pi r^{2}$

$=\frac{1}{6} \times 3.14 \times(10)^{2}$

$=52.33 \mathrm{~cm}^{2}$

In ΔOPQ,
∠OPQ = ∠OQP     (As OP = OQ)
∠OPQ + ∠OQP + ∠POQ = 180°
2∠OPQ = 120°
∠OPQ = 60°
ΔOPQ is an equilateral triangle.
So, area of ΔOPQ

$=\frac{\sqrt{3}}{4} \times(\text { Side })^{2}$

$=\frac{\sqrt{3}}{4} \times(10)^{2}$

$=\frac{100 \sqrt{3}}{4} \mathrm{~cm}^{2}$

$=43.30 \mathrm{~cm}^{2}$

Area of minor segment PRQ
= Area of sector OPRQ − Area of ΔOPQ
= 52.33 − 43.30
= 9.03 cm2

Area of major segment PSQ
= Area of circle − Area of minor segment PRQ

$=\pi(10)^{2}-9.03$

$=314-9.03$

$=304.97 \mathrm{~cm}^{2}$