A circle has its centre at the origin and a point

True

First,we draw a circle and a point from the given information

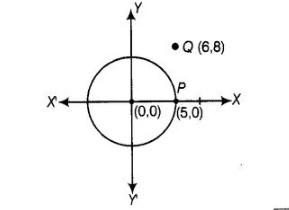
Now, distance between origin i.e., $O(0,0)$ and $P(5,0), O P=\sqrt{(5-0)^{2}+(0-0)^{2}}$

$\left[\because\right.$ Distance between two points $\left(x_{1}, y_{1}\right)$ and $\left.\left(x_{2}, y_{2}\right), d=\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}\right]$

$=\sqrt{5^{2}+0^{2}}=5=$ Radius of circle and distance between origin $O(0,0)$

and $Q(6,8), O Q=\sqrt{(6-0)^{2}+(8-0)^{2}}=\sqrt{6^{2}+8^{2}}=\sqrt{36+64}=\sqrt{100}=10$

We know that, if the distance of any point from the centre is less than/equal to/ more than the radius, then the point is inside/on/outside the circle,

respectively.

Here, we see that, OQ > OP

Hence, it is true that point Q (6, 8), lies outside the circle.