A circle touches the y-axis at the point

Solution:

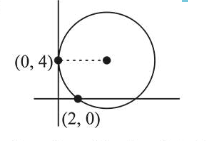
Equation of family of circle

$(x-0)^{2}+(y-4)^{2}+\lambda x=0$

Passes through the point $(2,0)$ then

$4+16+2 \lambda=0 \Rightarrow \lambda=-10$

Hence, the equation of circle

$x^{2}+y^{2}-10 x-8 y+16=0$

$\Rightarrow(x-5)^{2}+(y-4)^{2}=25$

Centre $(5,4)$.

$R=\sqrt{\frac{1}{2} \text { coeff. of } x+\frac{1}{2} \text { coeff. of } y \text {-constant }}$

$=\sqrt{25+16-16}=5$

Perpendicular distance of $4 x+3 y-8=0$ from the centre of circle

$=\left|\frac{20+16-8}{\sqrt{16+9}}\right|=\frac{28}{5} \neq 5$

Hence, $4 x+3 y-8=0$ can not be tangent to the circle.