A circle touching the x-axis at (3,0)

A circle touching the $x$-axis at $(3,0)$ and making an intercept of length 8 on the $y$-axis passes through the point :

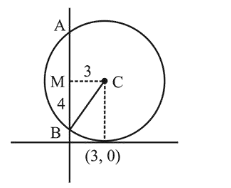
$C B=\sqrt{M C^{2}+M B^{2}}$

$\sqrt{3^{2}+4^{2}}=5=$ radius of circle

$\therefore$ equation of circle is,

$(x-3)^{2}+(y-5)^{2}=5^{2}$

$(3,10)$ satisfies this equation.

Although there will be another circle satisfying the same conditions that will lie below the $x$-axis having equation $(x-3)^{2}+(y-5)^{2}=5^{2}$