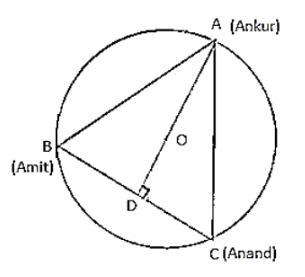
A circular park of radius 40 m is situated in a colony. Three boys Ankur, Amit and Anand are sitting at equal distance on its boundary each having a toy telephone in his hands to talk to each other. Find the length of the string of each phone.
Given that AB = BC = CA
So, ABC is an equilateral triangle
OA (radius) = 40 m
Medians of equilateral triangle pass through the circum centre (O) of the equilateral triangle ABC.
We also know that median intersect each other at the ratio 2: 1.
As AD is the median of equilateral triangle ABC, we can write:
OA/OD = 2/1
⇒ 4OM/OD = 2/1
⇒ OD = 20m
Therefore, AD = OA + OD = (40 + 20) m
= 60 m
In ΔADC
By using Pythagoras theorem
$A C^{2}=A D^{2}+D C^{2}$
$A C^{2}=60^{2}+\left(A C^{2}\right)^{2}$
$A C^{2}=3600+A C^{2} / 4$
$\Rightarrow 3 / 4 \mathrm{AC}^{2}=3600$
$\Rightarrow \mathrm{AC}^{2}=4800$
$\Rightarrow A C=40 \sqrt{3} \mathrm{~m}$
So, length of string of each phone will be 40√3 m.
