A circular pond is 17.5 m is of diameter.

Given that, a circular pond is surrounded by a wide path.
The diameter of circular pond = 17.5 m

$\therefore \quad$ Radius of circular pond $\left(r_{i}\right)=\frac{\text { Diameter }}{2}$

i.e., $O A=r_{i}=\frac{17.5}{2}=8.75 \mathrm{~m}$

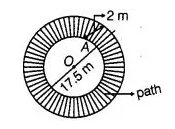
and the width of the path $=2 \mathrm{~m}$

i.e. $A B=2 \mathrm{~m}$

Now, $\quad$ length of $O B=O A+A B=r_{j}+A B$

Let $\left(r_{e}\right)=8.75+2=10.75 \mathrm{~m}$

So, area of circular path = Area of outer circle i.e., (circular pond + path)

- Area of circular pond

$=\pi r_{e}^{2}-\pi r_{i}^{2} \quad\left[\because\right.$ area of circle $\left.=\pi r^{2}\right]$

$=\pi\left(r^{2}-r_{i}^{2}\right)$

$=\pi\left\{(10.75)^{2}-(8.75)^{2}\right\}$

$=\pi\{(10.75+8.75)(10.75-8.75)\}$

$=3.14 \times 19.5 \times 2$

$=122.46 \mathrm{~m}^{2}$

Now, cost of constructing the path per square metre $=₹ 25$

$\therefore$ Cost constructing the path $₹ 122.46 \mathrm{~m}^{2}=122.46 \times 25$

$=₹ 3061.50$

Hence, required cost of constructing the path at the rate of $₹ 25$ per $\mathrm{m}^{2}$ is $₹ 3061.50$.