A class has 175 students. The following description gives the number of

Given:

- Number of students in class $=175$

- Number of students enrolled in Mathematics $=100$

- Number of students enrolled in Physics $=70$

- Number of students enrolled in Chemistry $=46$

- Number of students enrolled in Mathematics and Physics $=30$

- Number of students enrolled in Physics and Chemistry $=23$

- Number of students enrolled in Mathematics and Physics $=28$

- Number of students enrolled in all three subjects $=18$

To find:

(i) Number of students enrolled in Mathematics alone, Physics alone and Chemistry alone

Venn diagram:

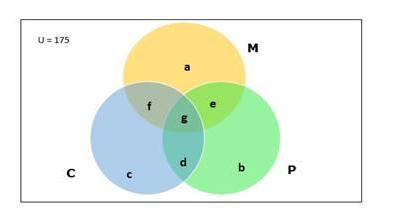
Number of students enrolled in Mathematics $=100=n(M)$

Number of students enrolled in Physics $=70=n(P)$

Number of students enrolled in Chemistry $=46=n(C)$

Number of students enrolled in Mathematics and Physics

$=30=n(M \cap P)$

Number of students enrolled in Mathematics and Chemistry

$=28=n(M \cap C)$

Number of students enrolled in Physics and Chemistry

$=23=n(P \cap C)$

Number of students enrolled in all the three subjects

$=18=n(M \cap P \cap C)=g$

We have

$n(M \cap P)=e+g$

$30=e+18$

$e=30-18=12$

$n(M \cap C)=f+g$

$28=f+18$

$f=28-18=10$

$n(P \cap C)=d+g$

$23=d+18$

$d=23-18=5$

a = Number of students enrolled only in Mathematics

b = Number of students enrolled only in Physicsc = Number of students enrolled only in Chemistry

We have,

$M=a+e+f+g$

$100=a+12+10+18$

$a=100-40$

$a=60$

Therefore,

Number of students enrolled only in Mathematics = 60

$P=b+e+d+g$

$70=b+12+5+18$

$b=70-35$

$b=35$

Therefore,

Number of students enrolled only in Physics = 35

$C=c+f+d+g$

$46=c+10+5+18$

$c=46-33$

$c=13$

Therefore,

Number of students enrolled only in Chemistry = 13

(ii) Number of students who have not offered any of these subjects

Number of students who have not offered any of these subjects

$=175-\{n(M)+n(P)+n(C)-n(M \cap P)-n(M \cap C)-n(P \cap C)+n(M \cap P \cap C)\}$

$=175-(100+70+46-30-28-23+18)$

$=175-153$

$=22$

Therefore

Number of students who have not offered any of these subjects = 22