A cone of radius 8 cm and height 12 cm

Let ORN be the cone then given, radius of the base of the cone r1 = 8cm

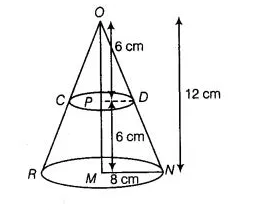
and height of the cone, $(h) O M=12 \mathrm{~cm}$ Let $P$ be the mid-point of $O M$, then

$O P=P M=\frac{12}{2}=6 \mathrm{~cm}$

Now, $\triangle O P D \sim \triangle O M N$

$\therefore \quad \frac{O P}{O M}=\frac{P D}{M N}$

$\Rightarrow \quad \frac{6}{12}=\frac{P D}{8} \Rightarrow \frac{1}{2}=\frac{P D}{8}$

$\Rightarrow \quad P D=4 \mathrm{~cm}$

The plane along CD divides the cone into two parts, namely

(i) a smaller cone of radius 4 cm and height 6cm and (ii) frustum of a cone for which

Radius of the top of the frustum, r1 = 4 cm

Radius of the bottom,r2 = 8 cm

and             height of the frustum, h = 6 cm

$\therefore \quad$ Volume of smaller cone $=\left(\frac{1}{3} \pi \times 4 \times 4 \times 6\right)=32 \pi \mathrm{cm}^{3}$

and volume of the frustum of cone $=\frac{1}{3} \times \pi \times 6\left[(8)^{2}+(4)^{2}+8 \times 4\right]$

$=2 \pi(64+16+32)=224 \pi \mathrm{cm}^{3}$

∴  Required ratio = Volume of frustum : Volume of cone = 24 π: 32 π = 1:7