Question.
A conical tent is 10 m high and the radius of its base is 24 m. Find
(i) slant height of the tent
(ii) cost of the canvas required to make the tent, if the cost of $1 \mathrm{~m}^{2}$ canvas is Rs 70 .
$\left[\right.$ Assume $\left.\pi=\frac{22}{7}\right]$
(i) slant height of the tent
(ii) cost of the canvas required to make the tent, if the cost of $1 \mathrm{~m}^{2}$ canvas is Rs 70 .
$\left[\right.$ Assume $\left.\pi=\frac{22}{7}\right]$
Solution:
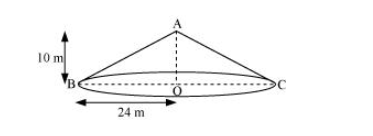
(i) Let ABC be a conical tent.
Height (h) of conical tent = 10 m
Radius (r) of conical tent = 24 m
Let the slant height of the tent be l.
In $\triangle \mathrm{ABO}$
$\mathrm{AB}^{2}=\mathrm{AO}^{2}+\mathrm{BO}^{2}$
$p^{2}=h^{2}+r^{2}$
$=(10 \mathrm{~m})^{2}+(24 \mathrm{~m})^{2}$
$=676 \mathrm{~m}^{2}$
$\therefore I=26 \mathrm{~m}$
Therefore, the slant height of the tent is 26 m.
(ii) CSA of tent $=\pi r l$
$=\left(\frac{22}{7} \times 24 \times 26\right) \mathrm{m}^{2}$
$=\frac{13728}{7} \mathrm{~m}^{2}$
Cost of $1 \mathrm{~m}^{2}$ canvas $=$ Rs 70
Cost of $\frac{13728}{7} \mathrm{~m}^{2}$ canvas $=\operatorname{Rs}\left(\frac{13728}{7} \times 70\right)$
$=\mathrm{Rs} 137280$
Therefore, the cost of the canvas required to make such a tent is
Rs 137280 .
(i) Let ABC be a conical tent.
Height (h) of conical tent = 10 m
Radius (r) of conical tent = 24 m
Let the slant height of the tent be l.
In $\triangle \mathrm{ABO}$
$\mathrm{AB}^{2}=\mathrm{AO}^{2}+\mathrm{BO}^{2}$
$p^{2}=h^{2}+r^{2}$
$=(10 \mathrm{~m})^{2}+(24 \mathrm{~m})^{2}$
$=676 \mathrm{~m}^{2}$
$\therefore I=26 \mathrm{~m}$
Therefore, the slant height of the tent is 26 m.
(ii) CSA of tent $=\pi r l$
$=\left(\frac{22}{7} \times 24 \times 26\right) \mathrm{m}^{2}$
$=\frac{13728}{7} \mathrm{~m}^{2}$
Cost of $1 \mathrm{~m}^{2}$ canvas $=$ Rs 70
Cost of $\frac{13728}{7} \mathrm{~m}^{2}$ canvas $=\operatorname{Rs}\left(\frac{13728}{7} \times 70\right)$
$=\mathrm{Rs} 137280$
Therefore, the cost of the canvas required to make such a tent is
Rs 137280 .