A cottage industry manufactures pedestal lamps and wooden shades, each requiring the use of a grinding/cutting machine and a sprayer. It takes 2 hours on grinding/cutting machine and 3 hours on the sprayer to manufacture a pedestal lamp. It takes 1 hour on the grinding/cutting machine and 2 hours on the sprayer to manufacture a shade. On any day, the sprayer is available for at the most 20 hours and the grinding/cutting machine for at the most 12 hours. The profit from the sale of a lamp is Rs 5 and that from a shade is Rs 3. Assuming that the manufacturer can sell all the lamps and shades that he produces, how should he schedule his daily production in order to maximize his profit?
Let the cottage industry manufacture x pedestal lamps and y wooden shades. Therefore,
x ≥ 0 and y ≥ 0
The given information can be compiled in a table as follows.
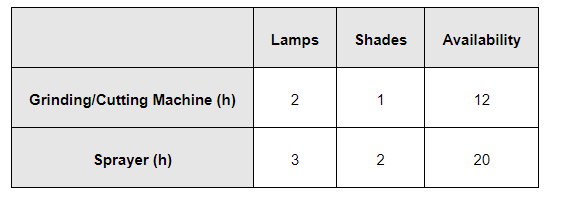
The profit on a lamp is Rs 5 and on the shades is Rs 3. Therefore, the constraints are
$2 x+y \leq 12$
$3 x+2 y \leq 20$
Total profit, $Z=5 x+3 y$
The mathematical formulation of the given problem is
Maximize $Z=5 x+3 y$ ...(1)
subject to the constraints,
$2 x+y \leq 12 \ldots$ (2)
$3 x+2 y \leq 20$ (3)
$x, y \geq 0 \ldots$ (4)
The feasible region determined by the system of constraints is as follows.
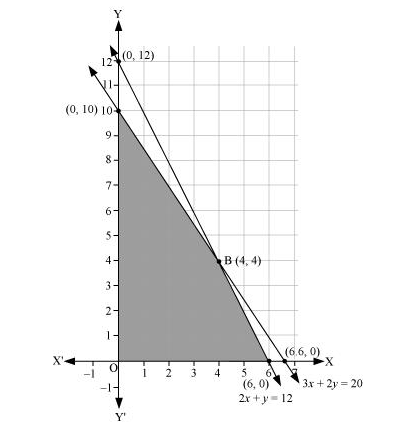
The corner points are A (6, 0), B (4, 4), and C (0, 10).
The values of Z at these corner points are as follows

The maximum value of Z is 32 at (4, 4).
Thus, the manufacturer should produce 4 pedestal lamps and 4 wooden shades to maximize his profits.
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.
