A cow is tied with a rope of length 14 m

Let ABCD be a rectangular field of dimensions 20 m x 16 m . Suppose, a cow is tied at a point A Let length of rope be AE = 14 m = r (say).

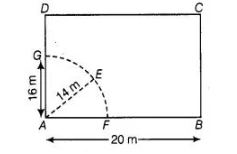
$\therefore$ Area of the field in which the cow graze $=$ Area of sector $A F E G=\frac{\theta}{360^{\circ}} \times \pi r^{2}$

$=\frac{90}{360} \times \pi(14)^{2}$

Iso, the angle between two adiacent sides of a rectangle is $90^{\circ}$ ]

$=\frac{1}{4} \times \frac{22}{7} \times 196$

$=154 \mathrm{~m}^{2}$