A cube of side b has a charge q at each of its vertices.

Length of the side of a cube = b

Charge at each of its vertices = q

A cube of side b is shown in the following figure.

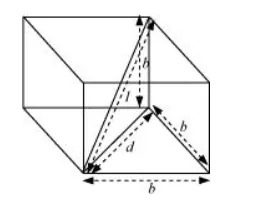
d = Diagonal of one of the six faces of the cube

$l^{2}=\sqrt{d^{2}+b^{2}}$

$d=b \sqrt{2}$

l = Length of the diagonal of the cube

$l^{2}=\sqrt{d^{2}+b^{2}}$

$=\sqrt{(\sqrt{2} b)^{2}}+b^{2}=\sqrt{2 b^{2}+b^{2}}=\sqrt{3 b^{2}}$

$l=b \sqrt{3}$

$r=\frac{l}{2}=\frac{b \sqrt{3}}{2}$ is the distance between the centre of the cube and one of the eight vertices

The electric potential (V) at the centre of the cube is due to the presence of eight charges at the vertices.

$V=\frac{8 q}{4 \pi \epsilon_{0}}$

$=\frac{8 q}{4 \pi \in_{0}\left(b \frac{\sqrt{3}}{2}\right)}$

$=\frac{4 q}{\sqrt{3} \pi \in_{0} b}$

Therefore, the potential at the centre of the cube is $\frac{4 q}{\sqrt{3} \pi \in_{0} b}$.

The electric field at the centre of the cube, due to the eight charges, gets cancelled. This is because the charges are distributed symmetrically with respect to the centre of the cube. Hence, the electric field is zero at the centre.