Acylinder of mass $10 \mathrm{~kg}$ and radius $15 \mathrm{~cm}$ is rolling perfectly on a plane of inclination $30^{\circ}$. The coefficient of static friction $\mu_{\mathrm{s}}=0.25$.
(a) How much is the force of friction acting on the cylinder?
(b) What is the work done against friction during rolling?
(c) If the inclination θ of the plane is increased, at what value of θ does the cylinder begin to skid, and not roll perfectly?
Mass of the cylinder, m = 10 kg
Radius of the cylinder, r = 15 cm = 0.15 m
Co-efficient of kinetic friction, $\mu_{\mathrm{k}}=0.25$
Angle of inclination, $\theta=30^{\circ}$
Moment of inertia of a solid cylinder about its geometric axis, $I=\frac{1}{2} m r^{2}$
The various forces acting on the cylinder are shown in the following figure:
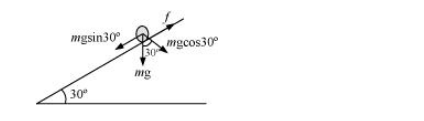
The acceleration of the cylinder is given as:
$a=\frac{m g \sin \theta}{m+\frac{I}{r^{2}}}$
$=\frac{m g \sin \theta}{m+\frac{1 m r^{2}}{2 r^{2}}}=\frac{2}{3} g \sin 30^{\circ}$
$=\frac{2}{3} \times 9.8 \times 0.5=3.27 \mathrm{~m} / \mathrm{s}^{2}$
(a) Using Newton's second law of motion, we can write net force as:
$f_{\text {net }}=m a$
$m g \sin 30^{\circ}-f=m a$
$=10 \times 9.8 \times 0.5-10 \times 3.27$
$=49-32.7=16.3 \mathrm{~N}$
(b) During rolling, the instantaneous point of contact with the plane comes to rest. Hence, the work done against frictional force is zero.
(c) For rolling without skid, we have the relation:
$\mu=\frac{1}{3} \tan \theta$
$\tan \theta=3 \mu=3 \times 0.25$
$\therefore \theta=\tan ^{-1}(0.75)=36.87^{\circ}$