A farmer buys a used for ₹180000. He pays ₹90000 in cash and agrees to pay the balance in annual instalments of ₹9000 plus 12% interest on the unpaid amount. How much did the tractor cost him?
Given: -
The amount that is to be paid to buy a tractor $=₹ 180000$.
An amount that he paid by cash $=₹ 90000$.
Remaining balance $=₹ 90000$
Annual instalment $=₹ 9000+$ interest @12\% on unpaid amount.
Thus, our instalments are 19800, 18720, 17640……
Total number of instalments =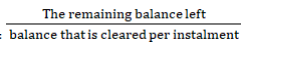 
$=\frac{90000}{9000}$
= 10
So our instalments are 19800, 18720, 17640 ... upto 10 terms.
All our instalments are in A.P with a common difference d.
Here
First term(a) = 19800
Common difference = d = 18720 - 19800
d = - 1080
Number of terms is 10
Sum of all instalments $=s_{n}=\frac{n}{2}\{2 \times a+(n-1) \times d\}$
$=\frac{10}{2}\{2 \times 19800+(10-1) \times(-1080)\}$
= 149400
Hence,
The total cost of the scooter = amount that is paid earlier + amount paid in 10 instalments.
= 90000 + 149400
∴The total cost paid by the farmer = ₹239400