Question.
A farmer moves along the boundary of a square field of side 10 m in 40 s. What will be the magnitude of displacement of the farmer at the end of 2 minutes 20 seconds ?
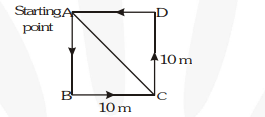
A farmer moves along the boundary of a square field of side 10 m in 40 s. What will be the magnitude of displacement of the farmer at the end of 2 minutes 20 seconds ?
Solution:
The perimeter of square field
$\mathrm{ABCD}=4 \times 10 \mathrm{~m}=40 \mathrm{~m}$.
Time for moving around the $10 \mathrm{~m}$ square field once $=40 \mathrm{~s}$.
Time for journey of farmer $=2 \mathrm{~min}$ and $20 \mathrm{~s}=140 \mathrm{~s}$.
Number of times the farmer moves around the square field $=\frac{140}{40}=3 \frac{1}{2}$ times.
For going once around the square field, the displacement $=0$
For going thrice around the square field, the displacement $=0$
For going $\frac{1}{2}$ around the square field, the distance covered $=40 \mathrm{~m} \times \frac{1}{2}=20 \mathrm{~m}$.
It is obvious from the figure, that if the farmer starts from point $\mathrm{A}$, then he will cover $10 \mathrm{~m}$ along $\mathrm{AB}$ and then $10
\mathrm{~m}$ along $\mathrm{BC}$.
Therefore, displacement of farmer from the point $A$ to point $C$ is
$$ \begin{aligned} A C=\sqrt{(A B)^{2}+(B C)^{2}} &=\sqrt{(10)^{2}+(10)^{2}}=\sqrt{200} \\ &=10 \sqrt{2}=14.14 \mathrm{~m} \end{aligned} $$
The perimeter of square field
$\mathrm{ABCD}=4 \times 10 \mathrm{~m}=40 \mathrm{~m}$.
Time for moving around the $10 \mathrm{~m}$ square field once $=40 \mathrm{~s}$.
Time for journey of farmer $=2 \mathrm{~min}$ and $20 \mathrm{~s}=140 \mathrm{~s}$.
Number of times the farmer moves around the square field $=\frac{140}{40}=3 \frac{1}{2}$ times.
For going once around the square field, the displacement $=0$
For going thrice around the square field, the displacement $=0$
For going $\frac{1}{2}$ around the square field, the distance covered $=40 \mathrm{~m} \times \frac{1}{2}=20 \mathrm{~m}$.
It is obvious from the figure, that if the farmer starts from point $\mathrm{A}$, then he will cover $10 \mathrm{~m}$ along $\mathrm{AB}$ and then $10
\mathrm{~m}$ along $\mathrm{BC}$.
Therefore, displacement of farmer from the point $A$ to point $C$ is
$$ \begin{aligned} A C=\sqrt{(A B)^{2}+(B C)^{2}} &=\sqrt{(10)^{2}+(10)^{2}}=\sqrt{200} \\ &=10 \sqrt{2}=14.14 \mathrm{~m} \end{aligned} $$