Question.
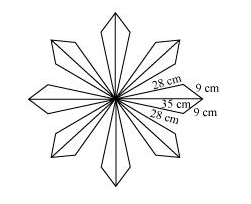
A floral design on a floor is made up of 16 tiles which are triangular, the sides of the triangle being 9 cm, 28 cm and 35 cm (see the given figure). Find the cost of polishing the tiles at the rate of 50p per cm2.

Solution:
It can be observed that
Semi-perimeter of each triangular-shaped tile, $s=\frac{(35+28+9) \mathrm{cm}}{2}=36 \mathrm{~cm}$
By Heron’s formula,
Area of triangle $=\sqrt{s(s-a)(s-b)(s-c)}$
Area of each tile $=[\sqrt{36(36-35)(36-28)(36-9)}] \mathrm{cm}^{2}$
$=[\sqrt{36 \times 1 \times 8 \times 27}] \mathrm{cm}^{2}$
$=36 \sqrt{6} \mathrm{~cm}^{2}$
$=(36 \times 2.45) \mathrm{cm}^{2}$
$=88.2 \mathrm{~cm}^{2}$
Area of 16 tiles $=(16 \times 88.2) \mathrm{cm}^{2}=1411.2 \mathrm{~cm}^{2}$
Cost of polishing per $\mathrm{cm}^{2}$ area $=50 \mathrm{p}$
Cost of polishing $1411.2 \mathrm{~cm}^{2}$ area $=$ Rs $(1411.2 \times 0.50)=$ Rs $705.60$
Therefore, it will cost Rs 705.60 while polishing all the tiles.
It can be observed that
Semi-perimeter of each triangular-shaped tile, $s=\frac{(35+28+9) \mathrm{cm}}{2}=36 \mathrm{~cm}$
By Heron’s formula,
Area of triangle $=\sqrt{s(s-a)(s-b)(s-c)}$
Area of each tile $=[\sqrt{36(36-35)(36-28)(36-9)}] \mathrm{cm}^{2}$
$=[\sqrt{36 \times 1 \times 8 \times 27}] \mathrm{cm}^{2}$
$=36 \sqrt{6} \mathrm{~cm}^{2}$
$=(36 \times 2.45) \mathrm{cm}^{2}$
$=88.2 \mathrm{~cm}^{2}$
Area of 16 tiles $=(16 \times 88.2) \mathrm{cm}^{2}=1411.2 \mathrm{~cm}^{2}$
Cost of polishing per $\mathrm{cm}^{2}$ area $=50 \mathrm{p}$
Cost of polishing $1411.2 \mathrm{~cm}^{2}$ area $=$ Rs $(1411.2 \times 0.50)=$ Rs $705.60$
Therefore, it will cost Rs 705.60 while polishing all the tiles.
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.
