Question:
A function $f$ is defined on $[-3,3]$ as
$f(x)=\left\{\begin{array}{cr}\min \left\{|x|, 2-x^{2}\right\}, & -2 \leq x \leq 2 \\ {[|x|]} & , 2<|x| \leq 3\end{array}\right.$
where $[\mathrm{x}]$ denotes the greatest integer $\leq \mathrm{x}$. The number of points, where $f$ is not differentiable in $(-3,3)$ is____.
Solution:
$f(x)=\left\{\begin{array}{ccc}\min \left\{|x|, 2-x^{2}\right\} & , & -2 \leq x \leq 2 \\ \||x|] & & 2<|x| \leq 3\end{array}\right.$
$\Rightarrow x \in[-3,-2) \cup(2,3]$
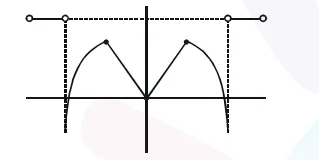
Number of points of non-differentiability in $(-3,3)=5$
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.