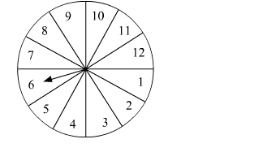
A game of chance consists of spinning an arrow which is equally likely to come to rest pointing to one of the numbers 1, 2, 3,..., 12 as shown in the figure.
A game of chance consists of spinning an arrow which is equally likely to come to rest pointing to one of the numbers 1, 2, 3,..., 12 as shown in the figure. What is the probability that it will point to
(i) 6?
(ii) an even number
(iii) a prime number?
(iv) a number which is a multiple of 5?
(v) a number which is a factor of 8?
The arrow can come to rest at any one of the numbers 1, 2, 3, 4,..., 12.
∴ Total number of outcomes = 12
(i) There is only one 6 in the figure. So, there is only one way when the arrow will come to rest pointing to the number 6.
Favourable number of outcomes = 1
$\therefore \mathrm{P}($ Arrow will point to 6$)=\frac{\text { Favourable number of outcomes }}{\text { Total number of outcomes }}=\frac{1}{12}$
(ii) There are six even numbers in the figure. These are 2, 4, 6, 8, 10 and 12. So, there are 6 ways when the arrow will come to rest pointing to an even number.
Favourable number of outcomes = 6
$\therefore \mathrm{P}$ (Arrow will point to an even number) $=\frac{\text { Favourable number of outcomes }}{\text { Total number of outcomes }}=\frac{6}{12}=\frac{1}{2}$
(iii) There are five prime numbers in the figure. These are 2, 3, 5, 7 and 11. So, there are 5 ways when the arrow will come to rest pointing to a prime number.
Favourable number of outcomes = 5
$\therefore \mathrm{P}($ Arrow will point to a prime number $)=\frac{\text { Favourable number of outcomes }}{\text { Total number of outcomes }}=\frac{5}{12}$
(iv) There are two multiples of 5 in the figure. These are 5 and 10. So, there are 2 ways when the arrow will come to rest pointing to a number which is a multiple of 5.
Favourable number of outcomes = 2
$\therefore P($ Arrow will point to a number which is a multiple of 5$)=\frac{\text { Favourable number of outcomes }}{\text { Total number of outcomes }}=\frac{2}{12}=\frac{1}{6}$
(v) There are four factors of 8 in the figure. These are 1, 2, 4 and 8. So, there are 4 ways when the arrow will come to rest pointing to a number which is a factor of 8.
Favourable number of outcomes = 4
$\therefore \mathrm{P}($ Arrow will point to a number which is a factor of 8$)=\frac{\text { Favourable number of outcomes }}{\text { Total number of outcomes }}=\frac{4}{12}=\frac{1}{3}$