A gulab jamun, contains sugar syrup up to about 30% of its volume.

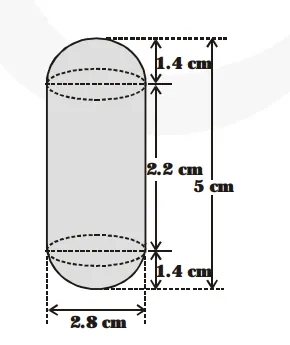
Since, a gulab jamun is like a cylinder with hemispherical ends.

Total height of the

gulab jamun = 5 cm.

Diameter = 2.8 cm

$\Rightarrow$ Radius $=1.4 \mathrm{~cm}$

$\therefore$ Length (height) of the cylindrical part

= 5cm – (1.4 + 1.4) cm = 5 cm – 2.8 cm = 2.2 cm

Now, volume of the cylindrical part $=\pi \mathrm{r}^{2} \mathrm{~h}$ and volume of both the hemispherical ends

$=2\left(\frac{2}{3} \pi \mathbf{r}^{3}\right)=\frac{4}{3} \pi \mathbf{r}^{3}$

$\therefore$ Volume of a gulab jamun

$=\pi r^{2} h+\frac{4}{3} \pi \mathbf{r}^{3}=\pi r^{2}\left[\mathbf{h}+\frac{4}{3} \mathbf{r}\right]$

$=\frac{22}{7} \times(1.4)^{2}\left[2.2+\frac{4}{3}(1.4)\right] \mathrm{cm}^{3}$

$=\frac{22}{7} \times \frac{14}{10} \times \frac{14}{10}\left[\frac{22}{10}+\frac{56}{30}\right] \mathrm{cm}^{3}$

$=\frac{22 \times 2 \times 14}{10 \times 10}\left[\frac{66+56}{30}\right] \mathrm{cm}^{2}$

$=\frac{44 \times 14}{100} \times \frac{122}{30} \mathrm{~cm}^{3}$

Volume of 45 gulab jamuns

$=45 \times\left[\frac{\mathbf{4 4} \times \mathbf{1 4}}{\mathbf{1 0 0}} \times \frac{\mathbf{1 2 2}}{\mathbf{3 0}}\right] \mathbf{c m}^{3}$

$=\frac{15 \times 44 \times 14 \times 122}{1000} \mathrm{~cm}^{3}$

Since, the quantity of syrup in gulab jamuns

= 30% of [volume]

$=30 \%$ of $\left[\frac{\mathbf{1 5} \times \mathbf{4 4} \times \mathbf{1 4} \times \mathbf{1 2 2}}{\mathbf{1 0 0 0}}\right] \mathrm{cm}^{3}$

$=\frac{\mathbf{3 0}}{\mathbf{1 0 0}} \times \frac{\mathbf{1 5} \times \mathbf{4 4} \times \mathbf{1 4} \times \mathbf{1 2 2}}{\mathbf{1 0 0 0}} \mathrm{cm}^{3}=338.184 \mathrm{~cm}^{3}$

$=338 \mathrm{~cm}^{2}$ (approx)