A hemisphere of maximum possible diameter is placed over a cuboidal block of side 7 cm.

(i) Disclaimer: It is written cuboid in the question but it should be cube.

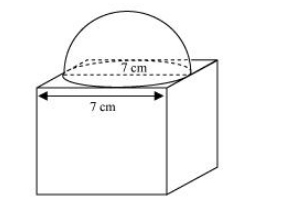
From the figure, it can be observed that the maximum diameter possible for such hemisphere is equal to the cube’s edge, i.e., 7 cm.

Radius $(r)$ of hemispherical part $=\frac{7}{2}=3.5 \mathrm{~cm}$

Total surface area of solid = Surface area of cubical part + CSA of hemispherical part

− Area of base of hemispherical part

$=6$ (Edge) $^{2}+2 \pi r^{2}-\pi r^{2}=6$ (Edge) $^{2}+\pi r^{2}$

Total surface area of solid $=6(7)^{2}+\frac{22}{7} \times \frac{7}{2} \times \frac{7}{2}$

$=294+38.5=332.5 \mathrm{~cm}^{2}$

(ii)

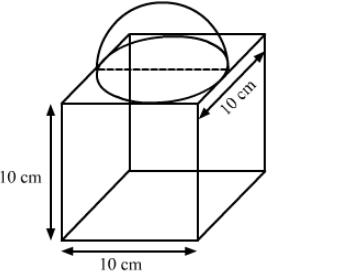
We have,

the edge of the cubical block, $a=10 \mathrm{~cm}$

The largest diameter of the hemisphere $=a=10 \mathrm{~cm}$

Also, the radius of the hemisphere, $r=\frac{10}{2}=5 \mathrm{~cm}$

Now,

Total surface area of the solid = TSA of cube + CSA of hemisphere-Area of circle

$=6 a^{2}+2 \pi r^{2}-\pi r^{2}$

$=6 a^{2}+\pi r^{2}$

$=6 \times 10 \times 10+3.14 \times 5 \times 5$

$=600+78.5$

$=678.5 \mathrm{~cm}^{2}$

As, the rate of painting the solid $=₹ 5$ per $100 \mathrm{~cm}^{2}$

So, the cost of painting the solid $=678.5 \times \frac{5}{100} \approx ₹ 33.92$

hence, the cost of painting the total surface area of the solid is ₹33.92.