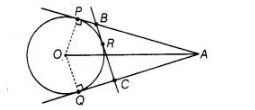
A is a point at a distance 13 cm

Solution:

Given Two tangents are drawn from an external point A to the circle with centre 0,

$O A=13 \mathrm{~cm}$

Tangent $B C$ is drawn at a point $R$. radius of circle equals $5 \mathrm{~cm}$. To find perimeter of $\triangle A B C$.

Proof $\angle O P A=90^{\circ}$

[tangent at any point of a circle is perpendicular to the radius through the point of contact]

 $\therefore$ $O A^{2}=O P^{2}+P A^{2}$ [by Pythagoras theorm]

$(13)^{2}=5^{2}+P A^{2}$

$\Rightarrow$ $P A^{2}=144=12^{2}$

$\Rightarrow \quad P A=12 \mathrm{~cm}$

Now, perimeter of $\triangle A B C=A B+B C+C A$ 

$=(A B+B R)+(R C+C A)$

 

$=A B+B P+C Q+C A$

$[\because B R=B P, A C=C Q$ tangents from internal point to a circle are equai]

$=A P+A Q$

$=2 A P$

$=2(12)$

 

$=24 \mathrm{~cm}$

$[A P=A Q$ tangent from internal point to a circle are equal]

Hence, the perimeter of $\triangle A B C=24 \mathrm{~cm}$.