A kite is 120 m high and 130 m of string is out.

In the right triangle $A B C$,

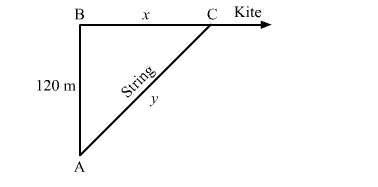
Here,

$A B^{2}+B C^{2}=A C^{2}$

$\Rightarrow x^{2}+(120)^{2}=y^{2}$

$\Rightarrow 2 x \frac{d x}{d t}=2 y \frac{d y}{d t}$

$\Rightarrow \frac{d y}{d t}=\frac{x}{y} \frac{d x}{d t}$

$\Rightarrow \frac{d y}{d t}=\frac{50}{130} \times 52$            $\left[\because x=\sqrt{(130)^{2}-(120)^{2}}=50\right]$

$\Rightarrow \frac{d y}{d t}=20 \mathrm{~m} / \mathrm{sec}$