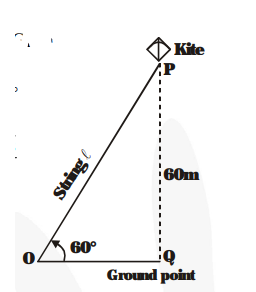
A kite is flying at a height of 60 m above the ground.

$P$ is the position of the kite. Its height from the point $Q$ (on the ground) $=P Q=60 \mathrm{~m}$

Let $O P=\ell$ be the length of the string.

$\angle \mathrm{POQ}=60^{\circ}$ (Given)

Now, $\frac{\mathbf{P Q}}{\mathbf{O P}}=\sin \mathbf{6 0}^{\circ}$

$\Rightarrow \frac{60}{\ell}=\sin 60^{\circ}=\frac{\sqrt{3}}{2}$

$\Rightarrow \frac{\mathbf{6 0}}{\ell}=\frac{\sqrt{3}}{2}$

$\Rightarrow \ell=40 \sqrt{3 m}$