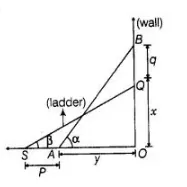
A ladder against a vertical wall at an inclination

Iet $\quad O O=x$ and $O A=v$

Given that, $B Q=q, S A=P$ and $A B=S Q=$ Length of ladder

Also, $\angle B A O=\alpha$ and $\angle Q S O=\beta$

Now, in $\triangle B A O$,

$\cos \alpha=\frac{O A}{\Delta R}$

$\Rightarrow$ $\cos \alpha=\frac{y}{A B}$

$\Rightarrow$ $y=A B \cos \alpha=O A$ $\ldots$ (i)

and  $\sin \alpha=\frac{O B}{A B}$

$\Rightarrow \quad O B=B A \sin \alpha$ .....(ii)

Now, in $\triangle Q S O$

$\cos \beta=\frac{O S}{S Q}$

$\Rightarrow \quad O S=S Q \cos \beta=A B \cos \beta$ $[\because A B=S Q] \ldots$ (iii)

and $\sin \beta=\frac{O Q}{S Q}$

$\Rightarrow \quad O Q=S Q \sin \beta=A B \sin \beta$ $[\because A B=S Q] \ldots$ (iv)

Now, $S A=O S-A O$

$P=A B \cos \beta-A B \cos \alpha$

$\Rightarrow \quad P=A B(\cos \beta-\cos \alpha)$    $\ldots(v)$

and $\quad B Q=B O-Q O$ 

$\Rightarrow \quad q=B A \sin \alpha-A B \sin \beta$

$\Rightarrow \quad q=A B(\sin \alpha-\sin \beta)$ $\ldots$ (vi)

Eq. (v) divided by Eq. (vi), we get

$\frac{p}{q}=\frac{A B(\cos \beta-\cos \alpha)}{A B(\sin \alpha-\sin \beta)}=\frac{\cos \beta-\cos \alpha}{\sin \alpha-\sin \beta}$

$\Rightarrow$ $\frac{p}{q}=\frac{\cos \beta-\cos \alpha}{\sin \alpha-\sin \beta}$

Hence proved.