A ladder is placed along a wall of a house such that its upper end is touching the top of the wall.

Let AB be the wall of height h m and C be the points, makes an angle 60° and foot of the ladder is 2m away from the wall. We have to find height of wall

In a triangle ABC, given that BC = 2m and angle C = 60°

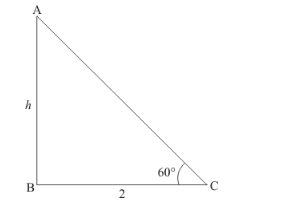
Now we have to find the height of wall.

So we use trigonometrically ratios.

In a triangle,

$\Rightarrow \quad \tan C=\frac{A B}{B C}$

$\Rightarrow \quad \tan 60^{\circ}=\frac{h}{2}$

$\Rightarrow \quad \sqrt{3}=\frac{h}{2}$

$\Rightarrow \quad h=2 \sqrt{3}$

Hence height of wall is $2 \sqrt{3}$ meters.