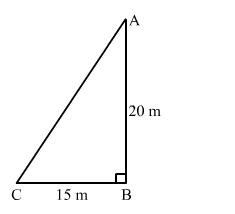
A ladder is placed in such a way that its foot is at a distance of 15 m from a wall and its top reaches a window 20 m above the ground.

Let the height of the window from the ground and the distance of the foot of the ladder from the wall be AB and BC, respectively.
We have:
AB = 20 m and BC = 15 m
Applying Pythagoras theorem in right-angled triangle ABC, we get:

$A C^{2}=A B^{2}+B C^{2}$

$\Rightarrow A C=\sqrt{20^{2}+15^{2}}$

$=\sqrt{400+225}$

$=\sqrt{625}$

$=25 m$

Hence, the length of the ladder is 25 m.