Question:
A light ray enters a solid glass sphere of refractive index $\mu=\sqrt{3}$ at an angle of incidence $60^{\circ}$. The ray is both reflected and refracted at the farther surface of the sphere. The angle (in degrees) between the reflected and refracted rays at this surface is
Solution:
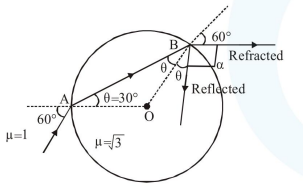
By Snell's law at $\mathrm{A}$ :
$1 \times \sin 60^{\circ}=\sqrt{3} \times \sin \theta$
$\frac{\sqrt{3}}{2}=\sqrt{3} \sin \theta$
$\sin \theta=\frac{1}{2} \Rightarrow \theta=30^{\circ}$
So at B :
$\theta+60^{\circ}+\alpha=180^{\circ}$
$30^{\circ}+60^{\circ}+\alpha=180^{\circ}$
$\alpha=90^{\circ}$
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.
