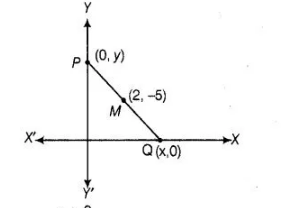
A line intersects the y-axis and X-axis at the points P and Q,

(d) Let the coordinates of P and 0 (0, y) and (x, 0), respectively.

So, the mid-point of $P(0, y)$ and $Q(x, 0)$ is $M\left(\frac{0+x}{2}, \frac{y+0}{2}\right)$

$\left[\because\right.$ mid-point of a line segment having points $\left(x_{1}, y_{1}\right)$ and $\left.\left(x_{2}, y_{2}\right)=\left(\frac{x_{1}+x_{2}}{2}, \frac{y_{1}+y_{2}}{2}\right)\right]$

But it is given that, mid-point of $P Q$ is $(2,-5)$.

$\therefore$ $2=\frac{x+0}{2}$

and $-5=\frac{y+0}{2}$

$\Rightarrow \quad 4=x$ and $-10=y$

$\Rightarrow \quad x=4$ and $y=-10$

So, the coordinates of P and Q are (0, -10) and (4, 0).