A line is a common tangent to the circle

Solution:

Let coordinate of point $\mathrm{A}\left(\mathrm{t}^{2}, 2 \mathrm{t}\right) \quad(\because \mathrm{a}=1)$ equation of tangent at point $\mathrm{A}$

$y t=x+t^{2}$

$x-t y+t^{2}=0$

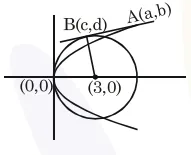
centre of circle $(3,0)$

Now PD = radius

$\left|\frac{3-0+t^{2}}{\sqrt{1+t^{2}}}\right|=3$

$\left(3+t^{2}\right)^{2}=9\left(1+t^{2}\right)$

$9+t^{4}+6 t^{2}=9+9 t^{2}$

$t=0,-\sqrt{3}, \sqrt{3}$

So point $\mathrm{A}(3,2 \sqrt{3})$

$\Rightarrow a=3, b=2 \sqrt{3}$

(Since it lies in first quadrant)

For point B which is foot of perpendicular from centre $(3,0)$ to the tangent $x-\sqrt{3} y+3=0$

$\frac{\mathrm{c}-3}{1}=\frac{\mathrm{d}-0}{-\sqrt{3}}=\frac{-(3-0+3)}{4}$

$\Rightarrow c=\frac{3}{2} \quad d=\frac{3 \sqrt{3}}{2}$

$\Rightarrow 2\left(\frac{3}{2}+3\right)=9$