A lot consists of 48 mobile phones of which 42 are good, 3 have only minor defects and 3 have major defects. Varnika will buy a phone, if it is good
but
the trader will only buy a mobile, if it has no major defect. One phone is selected at random from the lot. What is the probability that it is
(i) acceptable to Varnika?
(ii) acceptable to the trader?
Given, total number of mobile phones
$n(S)=48$
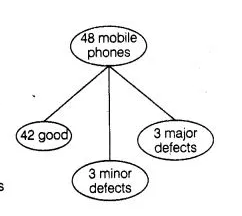
(I) Let $E_{1}=$ Event that Varnika will buy a mobile phone
$=$ Varnika buy only, if it is good mobile
$\therefore \cap\left(E_{1}\right)=42$
$\therefore P\left(E_{1}\right)=\frac{n\left(E_{1}\right)}{n(S)}=\frac{42}{48}=\frac{7}{8}$
(ii) Let $E_{2}=$ Event that trader will buy only when it has no major defects
$=$ Trader will buy only 45 modiles
$\therefore \quad n\left(E_{2}\right)=45$
$\therefore \quad P\left(E_{2}\right)=\frac{n\left(E_{2}\right)}{n(S)}=\frac{45}{48}=\frac{15}{16}$
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.
