A man 180 cm tall walks at a rate of 2 m/sec. away, from a source of light that is 9 m above the ground. How fast is the length of his shadow increasing when he is 3 m away from the base of light?
Let AB be the lamp post. Suppose at any time t, the man CD is at a distance x km from the lamp post and y m is the length of his shadow CE.
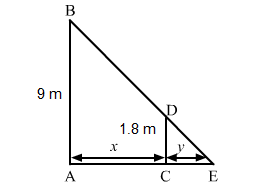
Since triangles $A B E$ and $C D E$ are similar,
$\frac{A B}{C D}=\frac{A E}{C E}$
$\Rightarrow \frac{9}{1.8}=\frac{x+y}{y}$
$\Rightarrow \frac{x}{y}=\frac{9}{1.8}-1$
$\Rightarrow \frac{x}{y}=\frac{7.2}{1.8}$
$\Rightarrow x=4 y$
$\Rightarrow \frac{d y}{d t}=\frac{1}{4}\left(\frac{d x}{d t}\right)$
$\Rightarrow \frac{d y}{d t}=\frac{1}{4} \times 2$ $\left(\because \frac{d x}{d t}=2\right)$
$\Rightarrow \frac{d y}{d t}=0.5 \mathrm{~m} / \mathrm{sec}$
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.
