A man is observing, from the top of a tower, a boat speeding towards the tower from a certain point $A$, with uniform speed. At that point, angle of depression of the boat with the man's eye is
$30^{\circ}$ (Ignore man's height). After sailing for 20 seconds, towards the base of the tower (which is at the level of water), the boat has reached a point $\mathrm{B}$, where the angle of depression is $45^{\circ}$. Then the time taken (in seconds) by the boat from $B$ to reach the base of the tower is:
Correct Option: , 3
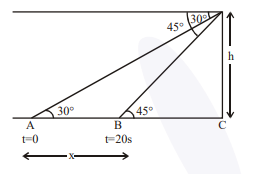
Let speed of boat is $\mathrm{u} \mathrm{m} / \mathrm{s}$ and height of tower is $\mathrm{h}$ meter \& distance $\mathrm{AB}=\mathrm{x}$ metre
$\therefore \mathrm{x}=\mathrm{h} \cot 30^{\circ}-\mathrm{h} \cot 45^{\circ}$
$\Rightarrow \mathrm{x}=\mathrm{h}(\sqrt{3}-1)$
$\therefore \mathrm{u}=\frac{\mathrm{x}}{20}=\frac{\mathrm{h}(\sqrt{3}-1)}{20} \mathrm{~m} / \mathrm{s}$
$\therefore$ Time taken to travel from $\mathrm{B}$ to $\mathrm{C}$ (Distance $=\mathrm{h}$ meter)
$=\frac{\mathrm{h}}{\mathrm{u}}=\frac{\mathrm{h}}{\mathrm{h} \frac{(\sqrt{3}-1)}{20}}=\frac{20}{\sqrt{3}-1}=10(\sqrt{3}+1) \mathrm{sec} .$
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.
