A man is observing, from the top of a tower, a boat speeding towards the tower from a certain point $\mathrm{A}$, with uniform speed. At that point, angle of depression of the boat with the man's eye is $30^{\circ}$ (Ignore man's height). After sailing for 20 seconds towards the base of the tower (which is at the level of water), the boat has reached a point $\mathrm{B}$, where the angle of depression is $45^{\circ}$. Then the time taken (in seconds) by the boat from B to reach the base of the tower is :
Correct Option: , 4
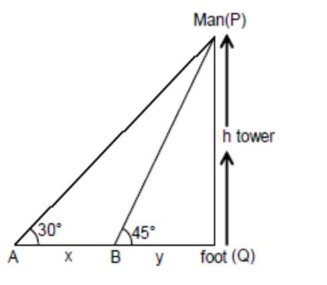
$\frac{\mathrm{h}}{\mathrm{x}+\mathrm{y}}=\tan 30^{\circ}$
$x+y=\sqrt{3} h$
Also
$\frac{\mathrm{h}}{\mathrm{y}}=\tan 45^{\circ}$
$\mathrm{h}=\mathrm{y}$
put in (1) $x+y=\sqrt{3} y$
$x=(\sqrt{3}-1) y$
$\frac{\mathrm{x}}{20}=^{\prime} \mathrm{v}^{\prime}$ speed
$\therefore$ time taken to reach
Foot from B
$\Rightarrow \frac{\mathrm{y}}{\mathrm{V}}$
$\Rightarrow \frac{x}{(\sqrt{3}-1) \cdot x} \times 20$
$\Rightarrow 10(\sqrt{3}+1)$
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.