A man of height 6 ft walks at a uniform speed of 9 ft/sec from a lamp fixed at 15 ft height. The length of his shadow is increasing at the rate of
(a) $15 \mathrm{ft} / \mathrm{sec}$
(b) $9 \mathrm{ft} / \mathrm{sec}$
(c) $6 \mathrm{ft} / \mathrm{sec}$
(d) none of these
(c) $6 \mathrm{ft} / \mathrm{sec}$
Let AB be the lamp post. Suppose at any time t, the man CD be at a distance of x km from the lamp post and y ft be the length of his shadow CE.
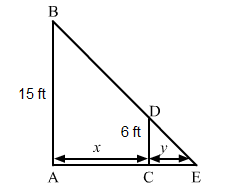
Since the triangles $A B E$ and $C D E$ are similar,
$\frac{A B}{C D}=\frac{A E}{C E}$
$\Rightarrow \frac{15}{6}=\frac{x+y}{y}$
$\Rightarrow \frac{x}{y}=\frac{15}{6}-1$
$\Rightarrow \frac{x}{y}=\frac{3}{2}$
$\Rightarrow y=\frac{2}{3} x$
$\Rightarrow \frac{d y}{d t}=\frac{2}{3}\left(\frac{d x}{d t}\right)$
$\Rightarrow \frac{d y}{d t}=\frac{2}{3} \times 9$
$\Rightarrow \frac{d y}{d t}=6 \mathrm{ft} / \mathrm{sec}$
