A man on the deck of a ship is 10 m above the water level. He observes that the

Let H be the height of the cliff CE. And a man is standing on the ships at the height of
10 meter above from the water level. Let AB = 10, BC = x, AD = BC, AB = DC, DE = h. and 

We have to find H and x

The corresponding figure is as follows

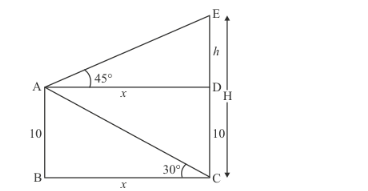
In $\triangle A B C$,

$\Rightarrow \quad \tan C=\frac{A B}{B C}$

$\Rightarrow \quad \tan 30^{\circ}=\frac{10}{x}$

$\Rightarrow \quad \frac{1}{\sqrt{3}}=\frac{10}{x}$

$\Rightarrow \quad x=10 \sqrt{3}$

Again in $\triangle D A E$,

$\Rightarrow \quad \tan A=\frac{D E}{A D}$

$\Rightarrow \quad \tan 45^{\circ}=\frac{h}{x}$

$\Rightarrow \quad \mathrm{I}=\frac{h}{x}$

$\Rightarrow \quad x=h$

$\Rightarrow x=10 \sqrt{3}$

Therefore $H=h+10$

$\Rightarrow \quad H=10 \sqrt{3}+10$

$\Rightarrow \quad H=10(\sqrt{3}+1)$

$\Rightarrow \quad H=27.32$

Hence the required distance is $10 \sqrt{3} \mathrm{~m}$. and height is $27.32 \mathrm{~m}$.