A man sitting at a height of 20 m on a tall tree on a small island in the middle of a river observes two poles directly opposite to each other on the two banks of the river and in line with the foot of tree. If the angles of depression of the feet of the poles from a point at which the man is sitting on the tree on either side of the river are 60° and 30°respectively. Find the width of the river.
Let 
be the width of river. And the angles of depression on either side of the river are 30° and 60° respectively. It is given that AC = 20 m. Let BC = x and CD = y. And 
, 
Here we have to find the width of river.
We have the corresponding figure as follows
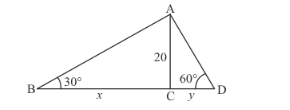
So we use trigonometric ratios.
In a triangle
,
$\Rightarrow \quad \tan B=\frac{A C}{B C}$
$\Rightarrow \quad \tan 30^{\circ}=\frac{20}{x}$
$\Rightarrow \quad \frac{1}{\sqrt{3}}=\frac{20}{x}$
$\Rightarrow \quad x=20 \sqrt{3}$
Again in a triangle 
$\Rightarrow \quad \tan D=\frac{A C}{C D}$
$\Rightarrow \quad \tan 60^{\circ}=\frac{20}{y}$
$\Rightarrow \quad \sqrt{3}=\frac{20}{y}$
$\Rightarrow \quad y=\frac{20}{\sqrt{3}}$
$\Rightarrow \quad x+y=20 \sqrt{3}+\frac{20}{20 \sqrt{3}}$
$\Rightarrow \quad x+y=\frac{80}{\sqrt{3}}$
Hence width of river is $\frac{80}{\sqrt{3}} \mathrm{~m}$.