A man travels 600 km partly by train and partly by car.

Let the speed of the train be x km/hr that of the car be y km/hr, we have the following cases:

Case I: When a man travels 600Km by train and the rest by car

Time taken by a man to travel $400 \mathrm{Km}$ by train $=\frac{400}{x} h r s$

Time taken by a man to travel $(600-400)=200 \mathrm{Km}$ by car $=\frac{200}{y}$ hrs

Total time taken by a man to cover $600 \mathrm{Km}=\frac{400}{x}+\frac{200}{y}$

It is given that total time taken in 8 hours

$\frac{400}{x}+\frac{200}{y}=6 h r s 30 \mathrm{~min}$

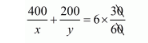
$\frac{400}{x}+\frac{200}{y}=6 \times \frac{1}{2}$

$\frac{400}{x}+\frac{200}{y}=\frac{13}{2}$

$200\left(\frac{2}{x}+\frac{1}{y}\right)=\frac{13}{2}$

$\left(\frac{2}{x}+\frac{1}{y}\right)=\frac{13}{2} \times \frac{1}{200}$

$\frac{2}{x}+\frac{1}{y}=\frac{13}{400} \cdots(i)$

Case II: When a man travels 200Km by train and the rest by car

Time taken by a man to travel $200 \mathrm{Km}$ by train $=\frac{200}{x} h r s$

Time taken by a man to travel $(600-200)=400 \mathrm{Km}$ by car $=\frac{400}{y} h r s$

In this case, total time of the journey in 6 hours 30 minutes + 30 minutes that is 7 hours,

$\frac{200}{x}+\frac{400}{y}=7$

$200\left(\frac{1}{x}+\frac{2}{y}\right)=7$

$\frac{1}{x}+\frac{2}{y}=\frac{7}{200}$..(ii)

Putting $\frac{1}{x}=u$ and,$\frac{1}{y}=u$, the equations ( $i$ ) and (ii) reduces to

$2 u+1 v=\frac{13}{400} \cdots(i i i)$

$1 u+2 v=\frac{7}{200} \cdots(v i)$

Multiplying equation (iii) by 6 the above system of equation becomes

$4 u+2 v=\frac{13}{200} \cdots(v)$

$1 u+2 v=\frac{7}{200} \cdots(v i)$

Substituting equation  and, we get

$4 u+2 v=\frac{13}{200}$

$\frac{1 u+2 v=\frac{7}{200}}{3 u=\frac{6}{200}}$

$u=\frac{6}{200} \times \frac{1}{3}$

$u=\frac{2}{200}$

$u=\frac{1}{100}$

Putting $u=\frac{1}{100}$ in equation $(v i)$, we get

$1 u+2 v=\frac{7}{200}$

$\frac{1}{100}+2 v=\frac{7}{200}$

$2 v=\frac{7}{200}-\frac{1}{100}$

$2 v=\frac{7}{200}-\frac{2}{200}$

$2 v=\frac{7-2}{200}$

$2 v=\frac{5}{200}$

$v=\frac{5}{200} \times \frac{1}{2}$

$v=\frac{1}{80}$

Now

$u=\frac{1}{100}$

$\frac{1}{x}=\frac{1}{100}$

$x=100$

and

$\nu=\frac{1}{80}$

$\frac{1}{y}=\frac{1}{80}$

$y=80$

Hence, the speed of the train is $100 \mathrm{kn} / \mathrm{hr}$,

The speed of the car is $80 \mathrm{~km} / \mathrm{hr}$