A mercury lamp is a convenient source for studying frequency dependence of photoelectric emission, since it gives a number of spectral lines ranging from the UV to the red end of the visible spectrum. In our experiment with rubidium photo-cell, the following lines from a mercury source were used:
λ1 = 3650 Å, λ2= 4047 Å, λ3= 4358 Å, λ4= 5461 Å, λ5= 6907 Å,
The stopping voltages, respectively, were measured to be:
V01 = 1.28 V, V02 = 0.95 V, V03 = 0.74 V, V04 = 0.16 V, V05 = 0 V
Determine the value of Planck’s constant h, the threshold frequency and work function for the material.
[Note: You will notice that to get h from the data, you will need to know e (which you can take to be 1.6 × 10−19 C). Experiments of this kind on Na, Li, K, etc. were performed by Millikan, who, using his own value of e (from the oil-drop experiment) confirmed Einstein’s photoelectric equation and at the same time gave an independent estimate of the value of h.]
Einstein’s photoelectric equation is given as:
$e V_{0}=h v-\phi_{0}$
$V_{0}=\frac{h}{e} v-\frac{\phi_{0}}{e}$ ....(1)
Where,
V0 = Stopping potential
h = Planck’s constant
e = Charge on an electron
ν = Frequency of radiation
$\phi_{0}=$ Work function of a material
It can be concluded from equation (1) that potential V0 is directly proportional to frequency ν.
Frequency is also given by the relation:
$v=\frac{\text { Speed of light }(c)}{\text { Wavelength }(\lambda)}$
This relation can be used to obtain the frequencies of the various lines of the given wavelengths.
$v_{1}=\frac{c}{\lambda_{1}}=\frac{3 \times 10^{8}}{3650 \times 10^{-10}}=8.219 \times 10^{14} \mathrm{~Hz}$
$v_{2}=\frac{c}{\lambda_{2}}=\frac{3 \times 10^{8}}{4047 \times 10^{-10}}=7.412 \times 10^{14} \mathrm{~Hz}$
$v_{3}=\frac{c}{\lambda_{3}}=\frac{3 \times 10^{8}}{4358 \times 10^{-10}}=6.884 \times 10^{14} \mathrm{~Hz}$
$v_{4}=\frac{c}{\lambda_{4}}=\frac{3 \times 10^{8}}{5461 \times 10^{-10}}=5.493 \times 10^{14} \mathrm{~Hz}$
$v_{5}=\frac{c}{\lambda_{5}}=\frac{3 \times 10^{8}}{6907 \times 10^{-10}}=4.343 \times 10^{14} \mathrm{~Hz}$
The given quantities can be listed in tabular form as:
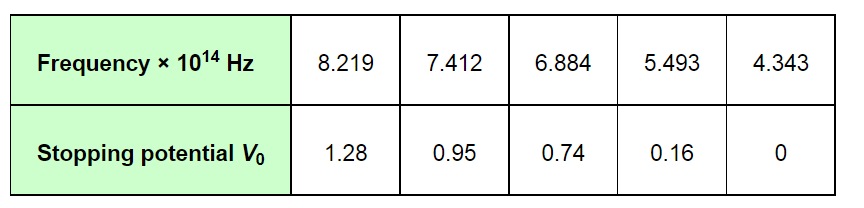
The following figure shows a graph between νand V0.
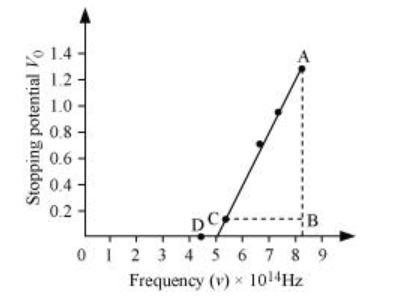
It can be observed that the obtained curve is a straight line. It intersects the ν-axis at 5 × 1014 Hz, which is the threshold frequency (ν0) of the material. Point D corresponds to a frequency less than the threshold frequency. Hence, there is no photoelectric emission for the λ5 line, and therefore, no stopping voltage is required to stop the current.
Slope of the straight line $=\frac{\mathrm{AB}}{\mathrm{CB}}=\frac{1.28-0.16}{(8.214-5.493) \times 10^{14}}$
From equation (1), the slope $\frac{h}{e}$ can be written as:
$\frac{h}{e}=\frac{1.28-0.16}{(8.214-5.493) \times 10^{14}}$
$\therefore h=\frac{1.12 \times 1.6 \times 10^{-19}}{2.726 \times 10^{14}}$
$=6.573 \times 10^{-34} \mathrm{Js}$
The work function of the metal is given as:
$\phi_{0}=h \mathrm{v}_{0}$
= 6.573 × 10−34 × 5 × 1014
= 3.286 × 10−19 J
$=\frac{3.286 \times 10^{-19}}{1.6 \times 10^{-18}}=2.054 \mathrm{eV}$
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.
