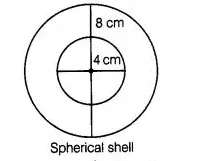
A metallic spherical shell of internal and external

(b) Given, internal diameter of spherical shell = 4 cm

and external diameter of shell = 8 cm

$\therefore$ Internal radius of spherical shell, $r_{1}=\frac{4}{2} \mathrm{~cm}=2 \mathrm{~cm}$ " $\quad[\because$ diameter $=2 \times$ radius $]$

and external radius of shell, $r_{2}=\frac{8}{2}=4 \mathrm{~cm}$ $[\because$ diameter $=2 \times$ radius $]$

Now, volume of the spherical shell $=\frac{4}{3} \pi\left[r_{2}^{3}-r_{1}^{3}\right]$

$\left[\because\right.$ volume of the spherical shell $=\frac{4}{3} \pi\left\{(\text { external radius })^{3}-\right.$ (internal radius) $\left.\left.^{3}\right\}\right]$

$=\frac{4}{3} \pi\left(4^{3}-2^{3}\right)$

$=\frac{4}{3} \pi(64-8)$

$=\frac{224}{3} \pi \mathrm{cm}^{3}$

Let height of the cone $=h \mathrm{~cm}$

Diameter of the base of cone $=8 \mathrm{~cm}$

$\therefore$ Radius of the base of cone $=\frac{8}{2}=4 \mathrm{~cm} \quad$ [\because\mathrm{ diameter } = 2 \times \text { radius } ]

According to the question,

Volume of cone $=$ Volume of spherical shell

$\Rightarrow \quad \frac{1}{3} \pi(4)^{2} h=\frac{224}{3} \pi \Rightarrow h=\frac{224}{16}=14 \mathrm{~cm}$

$\left[\because\right.$ volume of cone $=\frac{1}{3} \times \pi \times(\text { radius })^{2} \times($ height $\left.)\right]$

Hence, the height of the cone is $14 \mathrm{~cm}$.