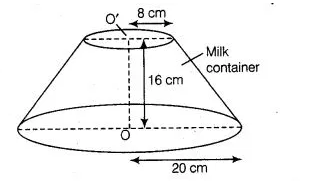
A milk container of height 16 cm is made of metal

Given that,height of milk container (h) = 16 cm,

Radius of lower end of milk container (r) = 8 cm

and radius of upper end of milk container (R) = 20 cm

$\therefore$ Volume of the milk container made of metal sheet in the form of a frustum of a cone

$=\frac{\pi h}{3}\left(R^{2}+r^{2}+R r\right)$

$=\frac{22}{7} \times \frac{16}{3}\left[(20)^{2}+(8)^{2}+20 \times 8\right]$

$=\frac{22 \times 16}{21}(400+64+160)$

$=\frac{22 \times 16 \times 624}{21}=\frac{219648}{21} \quad\left[\because 1 \mathrm{~L}=1000 \mathrm{~cm}^{3}\right]$

$=10459.42 \mathrm{~cm}^{3}=10.45942 \mathrm{~L}$

So, volume of the milk container is $10459.42 \mathrm{~cm}^{3}$.

$\because$ Cost of $1 \mathrm{~L}$ milk $=₹ 22$

$\therefore$ Cost of $10.45942 \mathrm{~L}$ milk $=22 \times 10.45942=₹ 230.12$

Hence, the required cost of milk is ₹ $230.12$