A particle of mass m is fixed to one end of a light spring having force constant k and unstretched length l.
Question:
A particle of mass $m$ is fixed to one end of a light spring having force constant $k$ and unstretched length $l$. The other end is fixed. The system is given an angular speed $\omega$ about the fixed end of the spring such that it rotates in a circle in gravity free space. Then the stretch in the spring is:
Correct Option: , 2
Solution:
(2) At elongated position $(x)$,
$F_{\text {radial }}=\frac{m v^{2}}{r}=m r \omega^{2}$
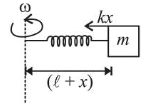
$\therefore k x=m(\ell+x) \omega^{2}$
$(\because r=\ell+x$ here $)$
$\mathrm{kx}=\mathrm{m} \ell \omega^{2}+\mathrm{mx} \omega^{2}$
$\therefore x=\frac{m \ell \omega^{2}}{k-m \omega^{2}}$
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.