A path of 4 m width runs round a semi-circular grassy plot

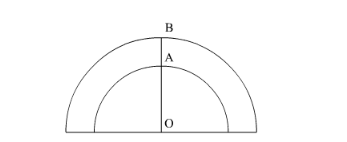
We have given $\mathrm{AB}=4 \mathrm{~m}$ and circumference of semicircle with radius $\mathrm{OA}$ as $163 \frac{3}{7} \mathrm{~m}$.

We are asked to find the area between the two semi-circles.

For that we will first find OA.

$\pi r=163 \frac{3}{7}$

Now we will substitute $\pi=\frac{22}{7}$

$\frac{22}{7} \times r=163 \frac{3}{7}$

$\Rightarrow r=52$

$\Rightarrow O A=52 \mathrm{~m}$

Now we will find OB.

$\therefore O B=A O+A B$

$\therefore O B=52+4$

$\therefore O B=56 \mathrm{~m}$

Now we will find the area between two semi-circles as given below,

$\therefore$ Area $=\frac{\pi \times 56 \times 56}{2}-\frac{\pi \times 52 \times 52}{2}$

$=\frac{\pi}{2}(1568-1352) \mathrm{m}^{2}$

$=\frac{\pi}{2} \times 216$

$=\frac{22}{7 \times 2} \times 216$

$=339.43 \mathrm{~m}^{2}$

Therefore, area of the path is $339.43 \mathrm{~m}^{2}$.

Now we will find the cost of gravelling the path.

Cost $=339.43 \times 1.50$

$=\operatorname{Rs} 509.14$

Therefore, cost of gravelling the path is Rs 509.14.

Now we will find the cost of turfing the plot. For that we will find the area of the plot.

Area of the plot $=\frac{1}{2} \pi r^{2}$

$=\frac{1}{2} \times \frac{22}{7}(52)^{2}$

$=\frac{1}{2} \times \frac{22}{7} \times 52 \times 52$

$=4249.14$

Cost of turfing the plot $=4249.14 \times 0.45$

$=\operatorname{Rs} 1912.11$

Therefore, cost of the turfing the plot is Rs 1912.11.
Disclaimer: Due to some error in the question, we get the different answers.