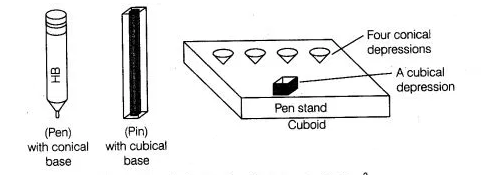
A pen stand made of wood is in the shap

Given that, length of cuboid pen stand (l) = 10 cm

Breadth of cubiod pen stand (b) = 5 c

and height of cuboid pen stand (h) = 4 cm

$\therefore$ Volume of cuboid pen stand $=l \times b \times h=10 \times 5 \times 4=200 \mathrm{~cm}^{3}$

Also, radius of conical depression $(r)=0.5 \mathrm{~cm}$ and height (depth) of a conical depression $\left(h_{1}\right)=2.1 \mathrm{~cm}$

$\therefore$ Volume of a conical depression $=\frac{1}{3} \pi r^{2} h_{1}$

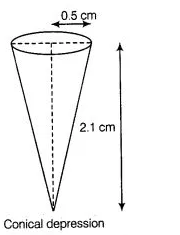
$=\frac{1}{3} \times \frac{22}{7} \times 0.5 \times 0.5 \times 2.1$

$=\frac{22 \times 5 \times 5}{1000}=\frac{22}{40}=\frac{11}{20}=0.55 \mathrm{~cm}^{3}$

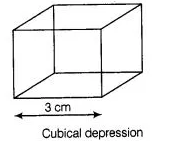
Also, given

Edge of cubical depression $(a)=3 \mathrm{~cm}$

$\therefore$ Volume of cubical depression $=(a)^{3}=(3)^{3}=27 \mathrm{~cm}^{3}$

So, volume of 4 conical depressions

$=4 \times$ Volume of a conical depression

$=4 \times \frac{11}{20}=\frac{11}{5} \mathrm{~cm}^{3}$

Hence, the volume of wood in the entire pen stand $=$ Volume of cuboid pen stand - Volume of 4 conical depressions - volume of a cubical depressions

$=200-\frac{11}{5}-27=200-\frac{146}{5}$

=200-29.2=170.8 \mathrm{~cm}^{3}

So, the required volume of the wood in the entire stand is 170.8 cm3.