A piece of wood of mass $6.03 \mathrm{~kg}$ is dropped from the top of a $100 \mathrm{~m}$ height building. At the same time, a bullet of mass $0.02 \mathrm{~kg}$ is fired vertically upward, with a velocity $100 \mathrm{~ms}^{-1}$, from the ground. The bullet gets embedded in the wood. Then the maximum height to which the combined system reaches above the top of the building before falling below is: $\left(\mathrm{g}=10 \mathrm{~ms}^{-2}\right)$
Correct Option:
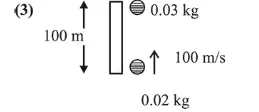
Time taken for the particles to collide,
$\mathrm{t}=\frac{\mathrm{d}}{\mathrm{V}_{\mathrm{rel}}}=\frac{100}{100}=1 \mathrm{sec}$
Speed of wood just before collision $=\mathrm{gt}=10 \mathrm{~m} / \mathrm{s}$
and speed of bullet just before collision $=\mathrm{v}-\mathrm{gt}$
$=100-10=90 \mathrm{~m} / \mathrm{s}$
$\mathrm{S}=100 \times 1-\frac{1}{2} \times 10 \times 1=95 \mathrm{~m}$
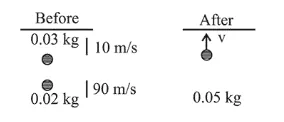
Now, using conservation of linear momentum just before and after the collision
$-(0.03)(10)+(0.02)(90)=(0.05) v$
$\Rightarrow 150=5 v$
$\therefore v=30 \mathrm{~m} / \mathrm{s}$
Max. height reached by body
$\mathrm{h}=\frac{\mathrm{g}}{2 \mathrm{~g}}=\frac{30 \times 30}{2 \times 10}=45 \mathrm{~m}$
$\therefore$ Height above tower $=40 \mathrm{~m}$
