A point charge $+10 \mu \mathrm{C}$ is a distance $5 \mathrm{~cm}$ directly above the centre of a square of side $10 \mathrm{~cm}$, as shown in Fig. 1.34. What is the magnitude of the electric flux through the square? (Hint: Think of the square as one face of a cube with edge $10 \mathrm{~cm}$.)
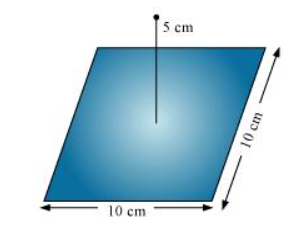
The square can be considered as one face of a cube of edge 10 cm with a centre where charge q is placed. According to Gauss’s theorem for a cube, total electric flux is through all its six faces.
$\phi_{\text {Total }}=\frac{q}{\epsilon_{0}}$
Hence, electric flux through one face of the cube i.e., through the square, $\phi=\frac{\phi_{\text {Total }}}{6}$
$=\frac{1}{6} \frac{q}{\epsilon_{0}}$
Where,
$\epsilon_{0}=$ Permittivity of free space
$=8.854 \times 10^{-12} \mathrm{~N}^{-1} \mathrm{C}^{2} \mathrm{~m}^{-2}$
$q=10 \mu \mathrm{C}=10 \times 10^{-6} \mathrm{C}$
$\therefore \phi=\frac{1}{6} \times \frac{10 \times 10^{-6}}{8.854 \times 10^{-12}}$
$=1.88 \times 10^{5} \mathrm{~N} \mathrm{~m}^{2} \mathrm{C}^{-1}$
Therefore, electric flux through the square is $1.88 \times 10^{5} \mathrm{~N} \mathrm{~m}^{2} \mathrm{C}^{-1}$.