A point E is taken on the side BC of a parallelogram ABCD.

Solution:

Given $A B C D$ is a parallelogram and $E$ is a point on $B C$. AE and DC are produced to meet at F. $A B \| C D$ anti $B C \| A D$, ..(i)

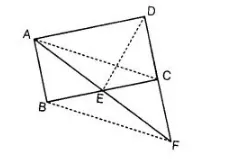
$\therefore$ $A B \| C D$ and $B C \| A D$ ...(i)

To prove $\operatorname{ar}(\triangle A D F)=\operatorname{ar}(A B F C)$

Construction Join $A C$ and $D E$.

Proof Since, $A C$ is a diagonal of parallelogram $A B C D$.

So, $\operatorname{ar}(\triangle A B C)=\operatorname{ar}(\triangle A C D)$ ...(ii)

Since, $\triangle A B F$ and $\triangle A B C$ are on the same base $A B$ and between the same parallels $A B$ and

$D F$. [since, $A B \| D C$ and $D C$ produced to $F$ ]

$\therefore \quad \operatorname{ar}(\Delta A B F)=\operatorname{ar}(\triangle A B C)$ ... (iii)

From Eqs. (ii) and (iii), 

$\operatorname{ar}(\triangle \mathrm{ABC})=\operatorname{ar}(\triangle \mathrm{ACD})=\operatorname{ar}(\triangle \mathrm{ABF})$

On subtracting ar $(\triangle A B E)$ from both sides of Eq. (iii), we get

$a r(\triangle A B F)-\operatorname{ar}(\triangle A B E)=\operatorname{ar}(\triangle A B C)-\operatorname{ar}(\triangle A B E)$

$\Rightarrow \quad \operatorname{ar}(\Delta B E F)=\operatorname{ar}(\triangle \mathrm{AEC})$ $\ldots(\mathrm{iv})$

Now, 

$\operatorname{ar}(A E C D)=\operatorname{ar}(A C D)+\operatorname{ar}(A E C)$

$=\operatorname{ar}(\Delta A B C)+\operatorname{ar}(\Delta B E F) \quad$ [from Eqs. (ii) and (iv)]

On adding ar $(\triangle C E F)$ both sides, we get

$\operatorname{ar}(A E C D)+\operatorname{ar}(\triangle C E F)$

$=\operatorname{ar}(\triangle A B C)+\operatorname{ar}(\triangle B E F)+\operatorname{ar}(\triangle C E F)$

$\Rightarrow \quad \operatorname{ar}(\triangle A D F)=\operatorname{ar}(A B F C) \quad$ Hence proved.