A point on the hypotenuse of a triangle is at distance a and b from the sides of the triangle.

Solution:

Let ΔABC be right-angled at B. Let AB = x and BC = y.

Let P be a point on the hypotenuse of the triangle such that P is at a distance of a and b from the sides AB and BC respectively.

Let ∠C = θ.

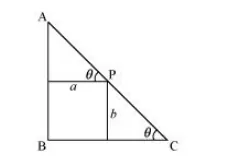
We have,

$\mathrm{AC}=\sqrt{x^{2}+y^{2}}$

Now,

PC = b cosec θ

And, AP = a sec θ

∴AC = AP + PC

$\Rightarrow \mathrm{AC}=b \operatorname{cosec} \theta+a \sec \theta \ldots$ (1)

$\therefore \frac{d(\mathrm{AC})}{d \theta}=-b \operatorname{cosec} \theta \cot \theta+a \sec \theta \tan \theta$

$\therefore \frac{d(\mathrm{AC})}{d \theta}=0$

$\Rightarrow a \sec \theta \tan \theta=b \operatorname{cosec} \theta \cot \theta$

$\Rightarrow \frac{a}{\cos \theta} \cdot \frac{\sin \theta}{\cos \theta}=\frac{b}{\sin \theta} \frac{\cos \theta}{\sin \theta}$

$\Rightarrow a \sin ^{3} \theta=b \cos ^{3} \theta$

$\Rightarrow(a)^{\frac{1}{3}} \sin \theta=(b)^{\frac{1}{3}} \cos \theta$

$\Rightarrow \tan \theta=\left(\frac{b}{a}\right)^{\frac{1}{3}}$

$\therefore \sin \theta=\frac{(b)^{\frac{1}{3}}}{\sqrt{a^{\frac{2}{3}}+b^{\frac{2}{3}}}}$ and $\cos \theta=\frac{(a)^{\frac{1}{3}}}{\sqrt{a^{\frac{2}{3}}+b^{\frac{2}{3}}}}$   ....(2)

It can be clearly shown that $\frac{d^{2}(\mathrm{AC})}{d \theta^{2}}<0$ when $\tan \theta=\left(\frac{b}{a}\right)^{\frac{1}{3}}$.

Therefore, by second derivative test, the length of the hypotenuse is the maximum when $\tan \theta=\left(\frac{b}{a}\right)^{\frac{1}{3}}$.

Now, when $\tan \theta=\left(\frac{b}{a}\right)^{\frac{1}{3}}$, we have:

$\mathrm{AC}=\frac{b \sqrt{a^{\frac{2}{3}}+b^{\frac{2}{3}}}}{b^{\frac{1}{3}}}+\frac{a \sqrt{a^{\frac{2}{3}}+b^{\frac{2}{3}}}}{a^{\frac{1}{3}}} \quad[$ Using (1) and (2) $]$

$=\sqrt{a^{\frac{2}{3}}+b^{\frac{2}{3}}}\left(b^{\frac{2}{3}}+a^{\frac{2}{3}}\right)$

$=\left(a^{\frac{2}{3}}+b^{\frac{2}{3}}\right)^{\frac{3}{2}}$

Hence, the maximum length of the hypotenuses is $\left(a^{\frac{2}{3}}+b^{\frac{2}{3}}\right)^{\frac{3}{2}}$.